隐含波动率代表预期,是当前期权市场的情绪。
期权链就像是一个坐标系一样,是一个平面。横轴是行权价,纵轴是到期日。每个点都是一对期权合约,由一个 Call 和一个 Put 组成。每个点有一个隐含波动率,把这些所有的点连在一起,就连成了一个曲面,这个曲面就叫 Vol Surface 波动率曲面,代表当前市场在每个点的不同情绪,而且这个隐含波动率曲面是立体的,每个市场每个期权链都有一个波动率曲面,隐含波动率曲面也是随着时间的流逝在不断变化。
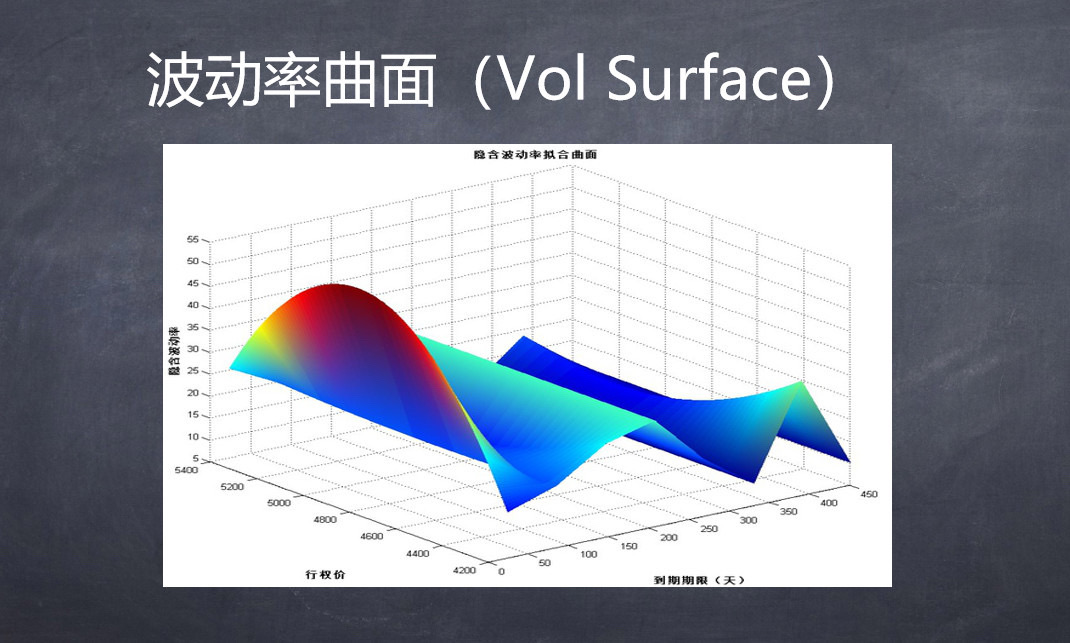
这个波动率曲面太复杂,不好研究,怎么办?降维。纵向切一刀,叫 Skew 曲线,从行权价的维度来研究就叫 Skew 曲线。横向切一刀,叫期限结构曲线,是在时间的维度进行研究。
比如 Skew 曲线,横轴是行权价,或者 Delta,纵轴是 IV。比如苹果 AAPL 的曲线,大家可以看出来,在现价附近 IV 最低,向上向下 IV 都在提高,这个就是波动率微笑 IV Smile,中间低两边高,是不是就像笑脸?根据理论上的假设,隐含波动率在不同行权价或者不同 Delta 值上的分布应该呈一条直线,但现实中常常出现不同行权价的期权隐含波动率变化的现象,使得曲线呈现“中间低、两头高”或向一端歪斜的形状,这种现象被称为“波动率微笑”或“波动率倾斜”。
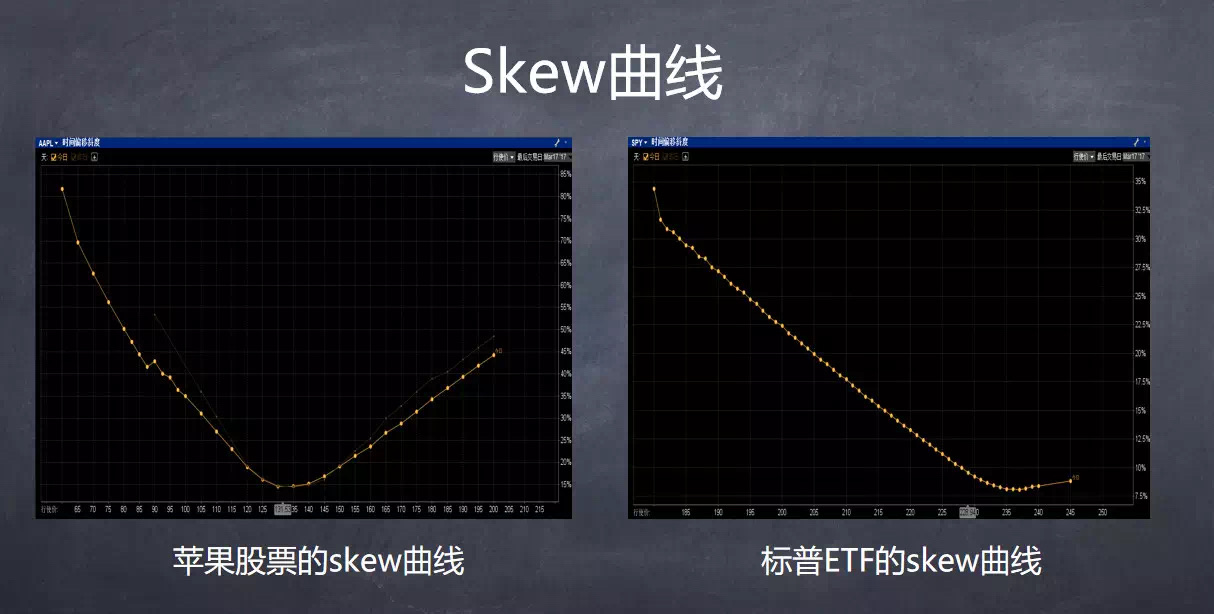
最早在1987年以前,曲线都是平的,因为B-S公式隐含了 Skew 曲线是平的,这会带来什么问题,就是低估了尾部风险事件发生的概率。因为这个概率是按照B-S公式正态分布计算的,所以真正尾部风险是严重低估的。几个西格玛(标准差)就动辄万年一遇,后来发现进来市场怎么总是遇到万年不遇的事情,这就是模型的问题。
真正的市场分布是遵循幂律分布的,他属于尖峰肥尾,尖峰还是很高,但是尾部并不低,尤其是下跌这个方向,出现极端的下跌的风险会比公式算出来更高一点。所以这就体现为,隐含波动率曲线上,在下方 Downside 这边,大家都愿意把期权的 IV 买的很贵,为什么?因为第一他发生的概率并没有公式描述的那么低,第二很多人愿意买保险,去买极端情况下的保险,觉得我能在极端情况下能活下来就行了。第三,有人愿意去赌黑天鹅事件,赌黑天鹅事件把这种方向的IV给推高了,所以下方的 IV 会很高,上方也会高一点,波动率微笑就是这么来的。
股票或股指的 Skew 曲线,一般的最低点不是现价,是比现价高一点,这是因为大量的机构在持有现货做Covered Call 备兑策略。所以大量机构卖的时候,就把隐含波动率曲线在现价上方卖出来一个低点。
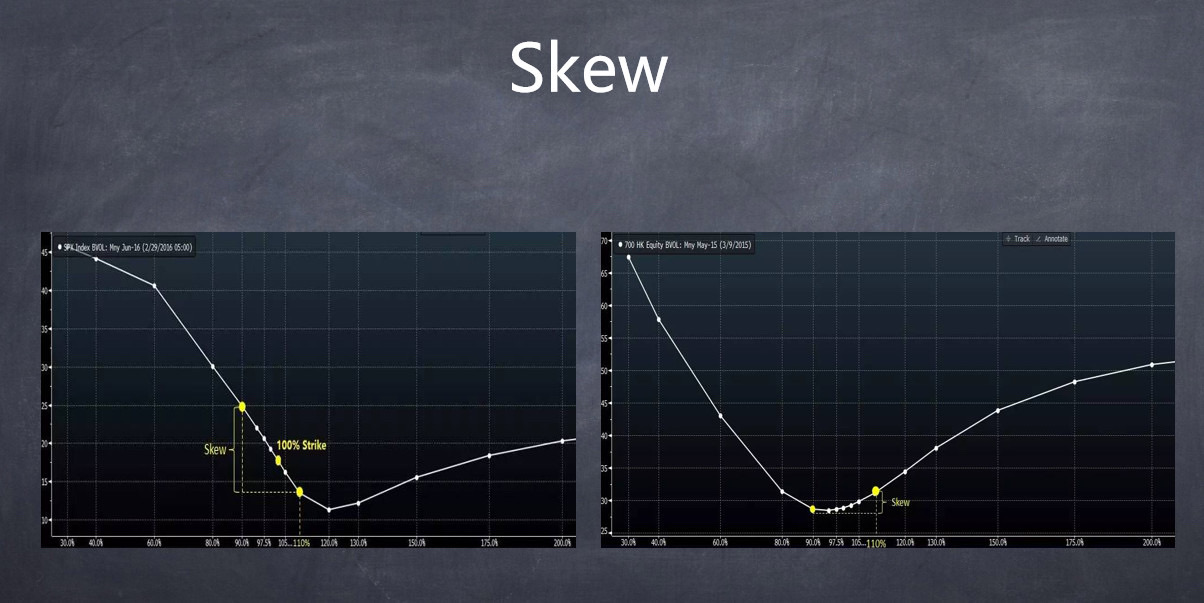
这个 Skew 曲线代表不同的行权价的市场情绪,市场目前的情绪对他的定价,越低代表这个位置现在市场给的定价是比较低的,预期没有太大波动,这个位置的期权比较便宜,高则反之。
这个曲线是不能预测未来的,它只反应当前的市场情绪。而且还有很重要一点,Skew 曲线是静态的,要从立体的角度动态来看它。比如,VIX 期权的 Skew 曲线是反过来的,Upside 上方很陡峭,Downside 下方不陡峭,很平缓。标普正好反过来:Downside下方陡峭,Upside不陡峭。大家要学会去动态的看,比如说,标普在T0 是100,T1 涨到110,Skew 曲线就会跟着往右偏移,这个时候你当时在 T0 买的90的 Put,随着标普的反弹,Skew 曲线整体向右移动,那么在 T0 时买的90 Put,在 T1 时 Skew 曲线对它的 IV 就会存在一个推升的作用。你要注意曲线不是静态的,是动态的。现价就是一个轴,当现价波动的时候,曲线也跟着动,这个时候是会带来一些盈利机会的。
做期权交易如何选择最优的行权价,从这个维度上去看更精细。这个空间存在一条 Skew 曲线,而且这个 Skew 曲线会随着标的的变化在震荡移动。除了空间以外,第二个维度也在变化,就是时间。接近到期的时候,Skew 曲线也会发生各种变化,或者扩大开口,或者缩小。不同的期权,股票的、期货的、指数的,变化规律都不太一样,每一类资产的期权链都有自己的规律。通过这个时间变化带来的 Skew 曲线的影响,又可以在期权交易上获得一点优势。
期权价格对 IV 非常敏感,波动率曲面的变化,在某个点带来的 IV 上升和下降的机会,如果善加利用,会对你的交易非常有好处的。
大家要理解,你的期权合约是有生命的,他的价格为什么会变?受到 Skew 曲线的影响,受到底层资产波动的影响,受到时间的影响,时间在变,空间也在变,时间空间一起变化,这些因素都会作用在这个波动率曲面上,最终这个曲面上每一个点的期权合约,价格就都开始波动了。脑子里要有这样一幅图画,才算真正进入波动率交易的殿堂。
期限结构:期权的期限结构曲线,横轴是不同合约的到期日,纵轴是IV,每个点就是市场对这个时间波动率市场的预期。期限结构上做的操作,一般来说是跨期操作,买近卖远或者卖近买远,表达不同的观点。
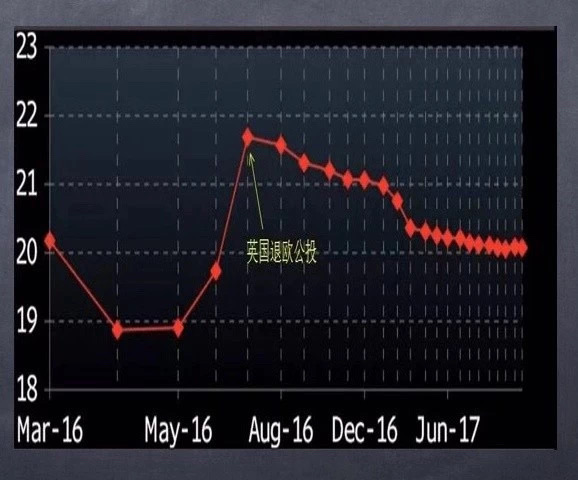
这两个曲线其实可以结合来看,会让你的期权交易变得更加精细。有时候我做一些操作,比如买实值的 Put,是可以优化到持有实值 Put 没有时间价值损耗的。当这个标的的 Skew 曲线,现价上方很陡峭,那么他只要稍微有点下跌,曲线就会变得更加陡峭,同样一个行权价,就是因为时间的推移,或者因为他下跌,带动的 Skew 曲线的变动,把我这个行权价的 IV 给推起来了,IV 的上升可以抵消掉我 Theta 的损耗,所以我就可以做到买方策略没有时间价值损耗。有些时候,当我去 Long 一些实值 Put 的或者实值 Call 的时候,我是有可能搞出正的时间价值来。但你公式上分析的肯定是负的时间价值,但是因为期限结构的变化、时间的推移以及SKEW的变化,你可以在已经很陡峭的点有了更陡峭的上升,带动整个SKEW曲线的变化,期权的买方策略也可以得到正的时间价值。
未经允许不得转载:美股开户者 » 讲期权 | Skew 曲线和期限结构曲线
 美股开户者
美股开户者