在这篇开始,我们先来用图来回顾下夏普比率。对于一个特定的资产组合1(持有股票A、B、 C),假定回测10年下来,组合1会产生2个关键的数据:收益和波动率。将收益作为纵坐标、波动率作为横坐标,在图表上做出组合1所在的点。
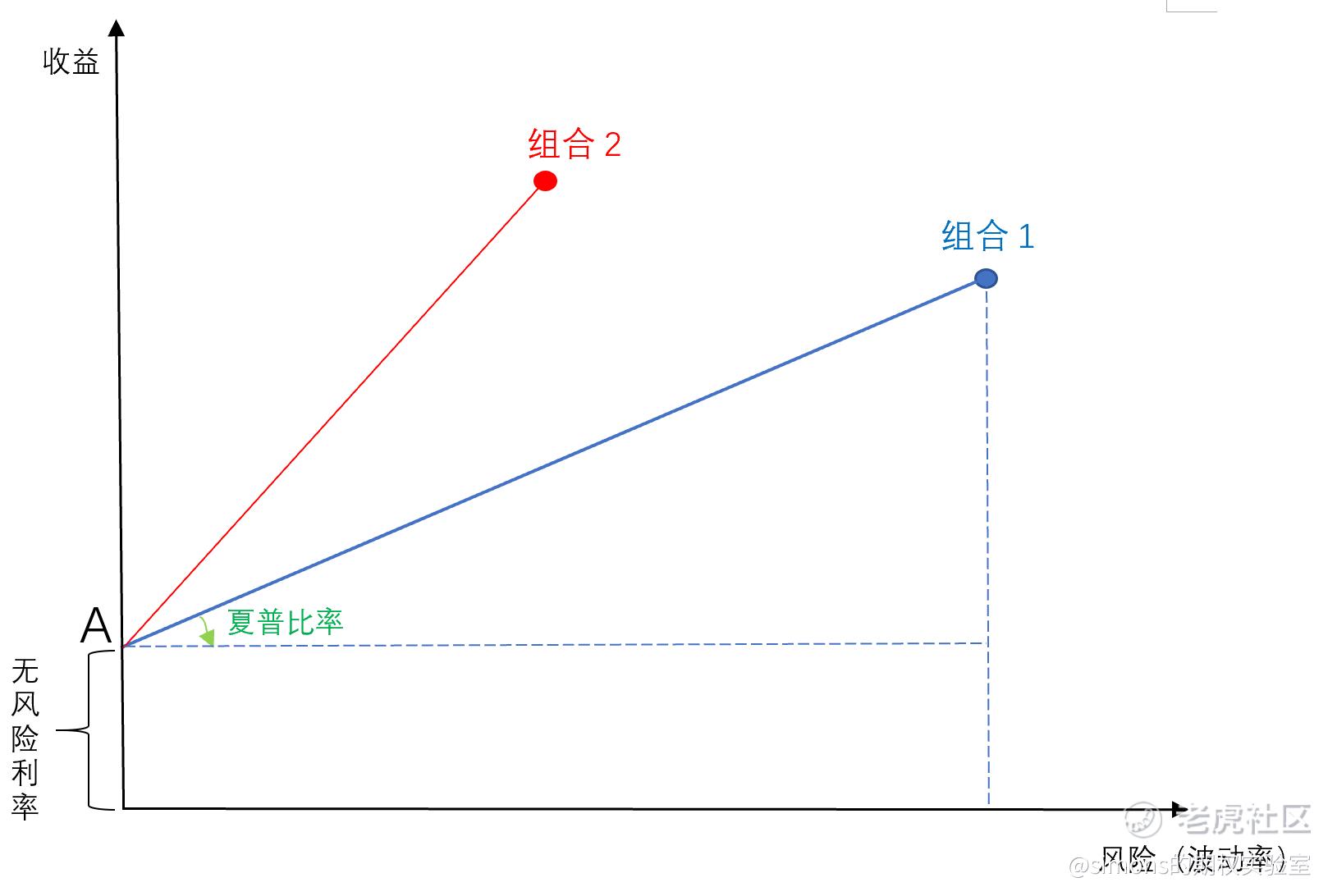
A点表示为无风险利率,(横坐标为0代表风险为0),一般以短期国债利率作为参考(目前为0.6%左右)。夏普比率就是(组合1收益-无风险利率)除以波动率的值。从图形上看,夏普比率即为A点到组合1线段的斜率。
任何投资者都应该在风险越低的情况下追求越高的收益。也就是说追求斜率越高越好。从图形上去好像挺简单,将组合1的斜率拉高至组合2就行了。但实际操作又是另一回事。一个成熟的投资者要将其收益斜率从1拉高至2,历程一定是非常艰辛的。
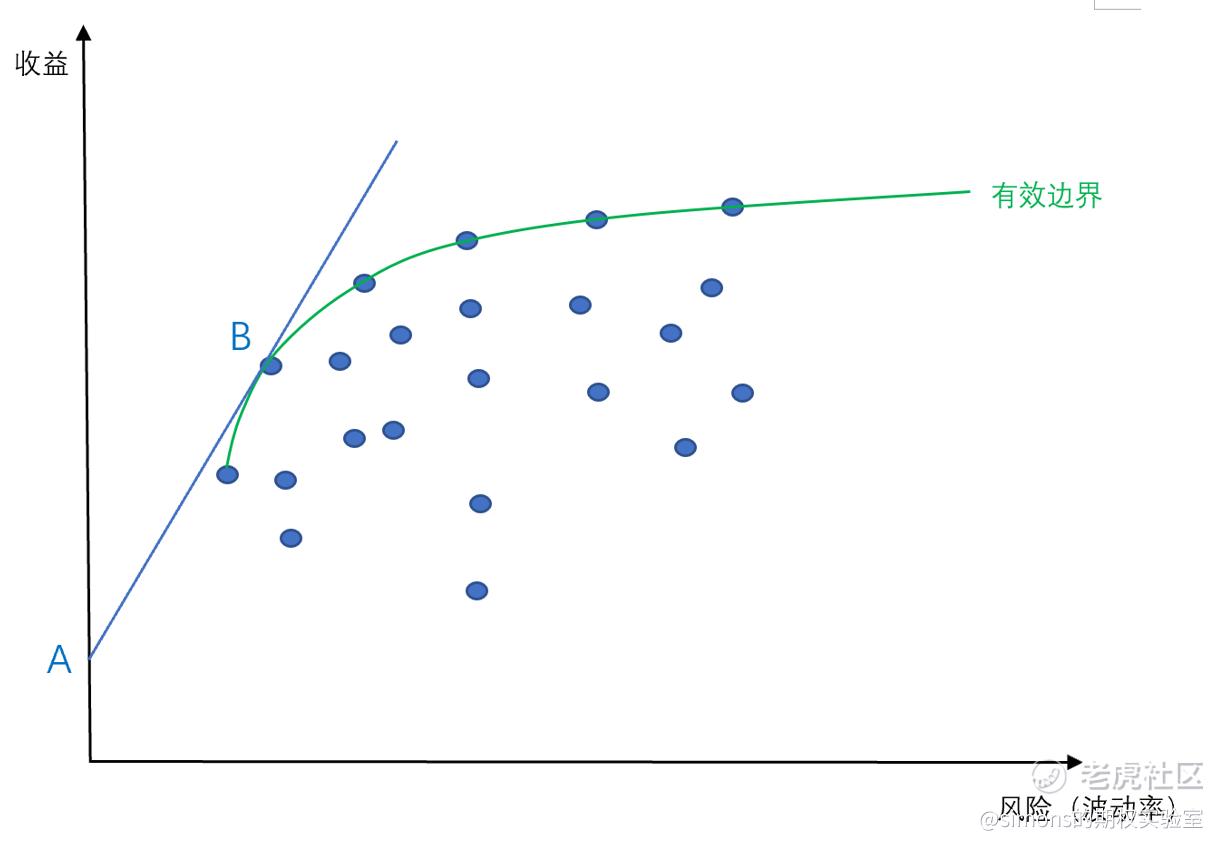
我们的主题是如何把夏普比率最大化,其实我们还是能从图中给出答案。我们回到有效边界的图(上图),从无风险利率A点开始拉一条线,与有效边界曲线相切,其切点即为最大夏普。假定这个有效边界的资产组合内含股票A、股票B、股票C,切点为这3只股票以任何比例所能达到的最大夏普比率。
按惯例,给个实例,以AAPL、SPY、TLT、TSLA、BAC作为我的股票池,用portfoliovisualizer计算出有效边界,如下图:最大夏普为:8.45%AAPL、7.55%BAC、7.14%TSLA、54.38%TLT、22.48SPY。
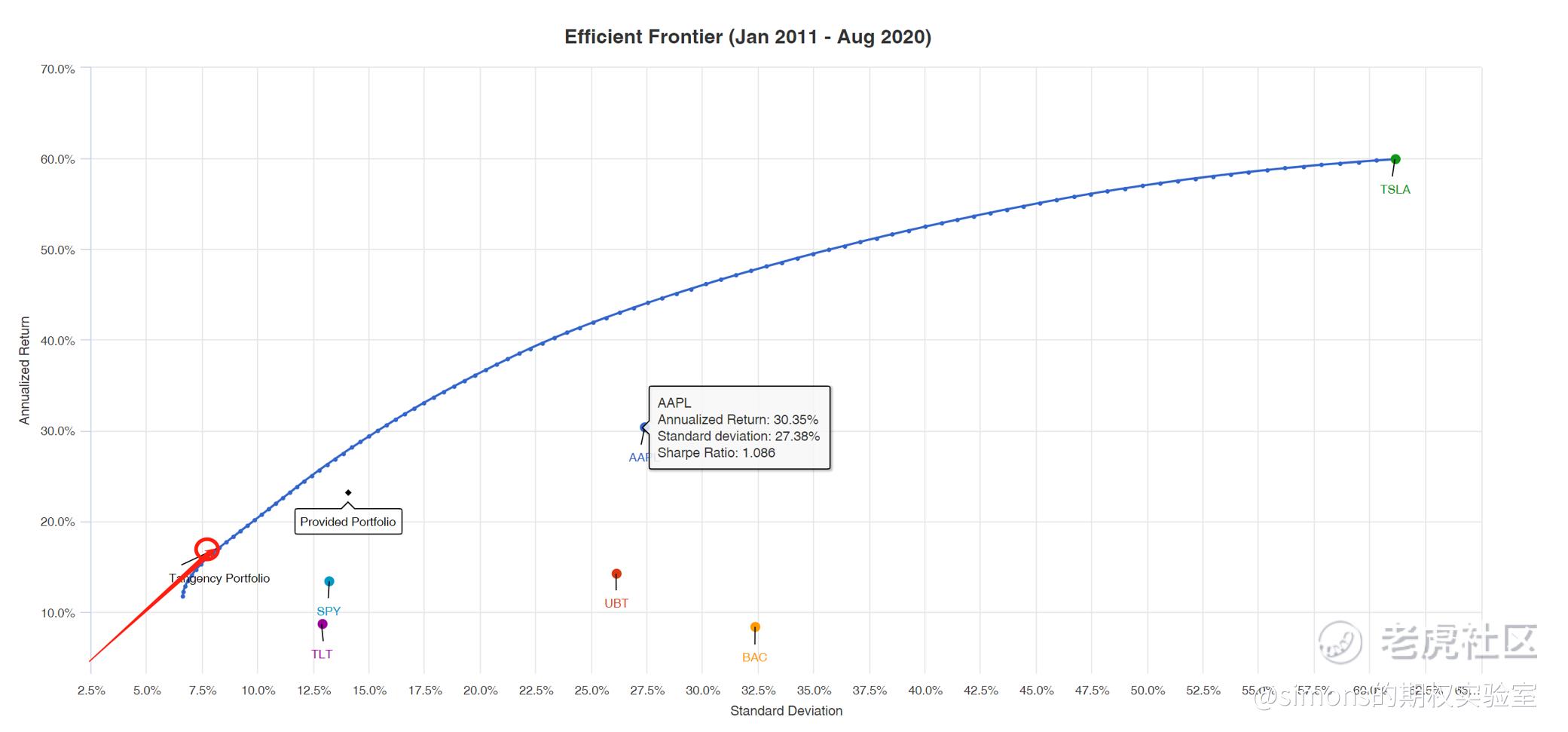
用软件自2011年开始回测该组合,表现如下:
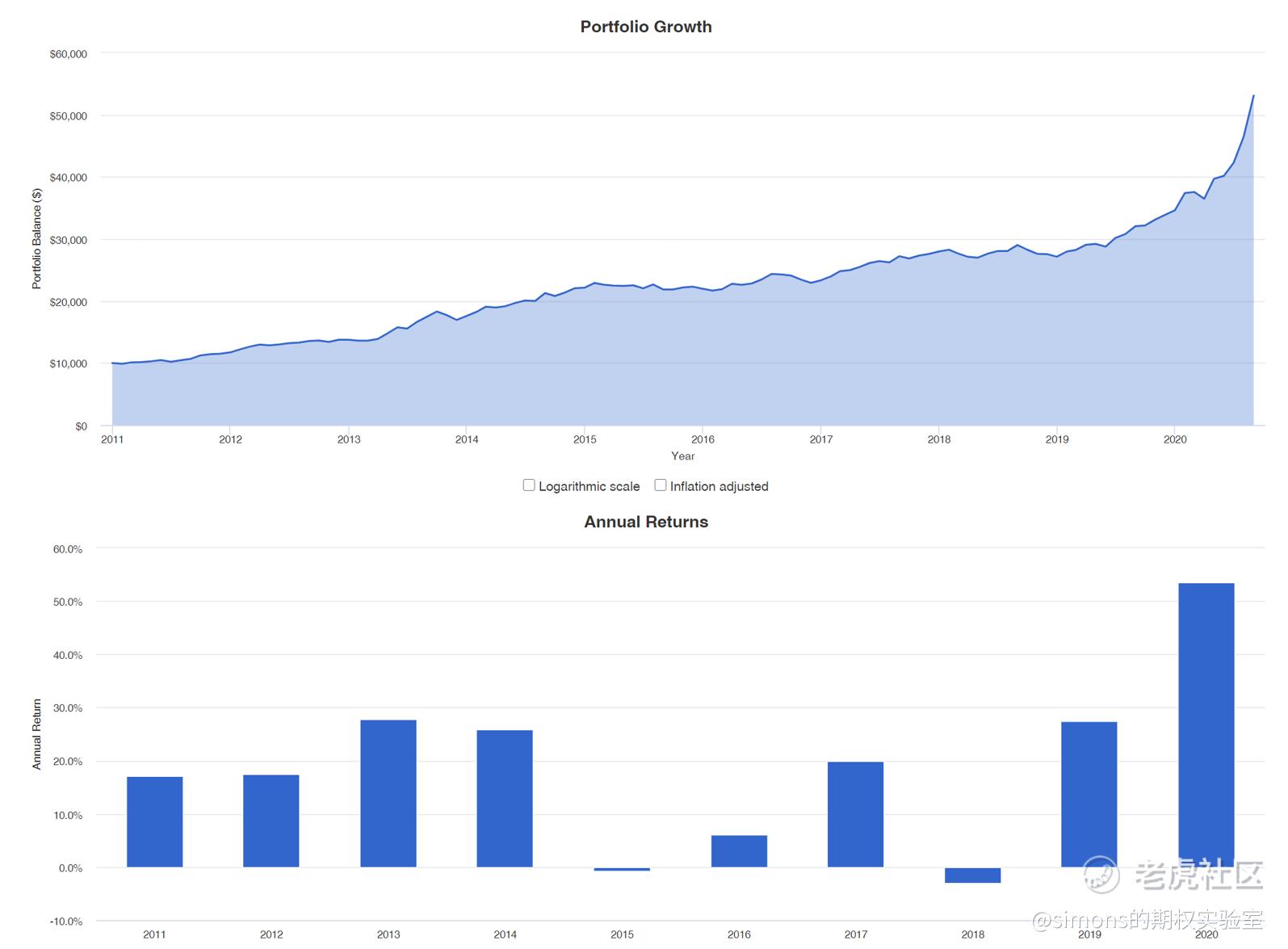
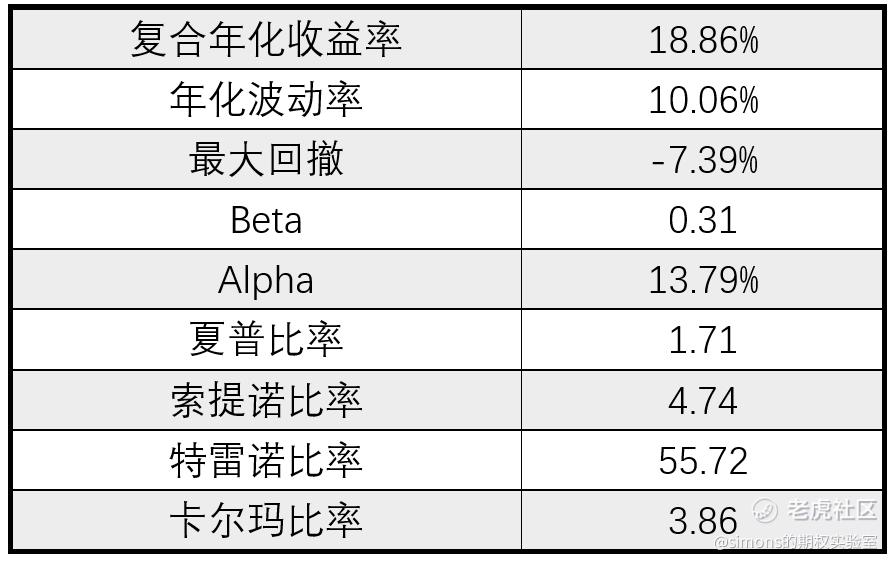
不要小看这个组合,如果过去按此组合加1倍杠杆,其复合年增长率CAGR已超过同时长期持有AAPL,(AAPL只有1.0左右的夏普),且beta只有0.31远低于AAPL,也就是说对大盘不敏感。以上只是举例,不构成投资建议。
未经允许不得转载:美股开户者 » 现代资产组合论(五)——最大夏普
 美股开户者
美股开户者